Арифметический квадратный корень. Свойства, правила, действия
Арифметическим квадратным корнем из числа а называется неотрицательное число b, квадрат которого равен а:
√а = b ( при a ≥ 0, b ≥ 0, b2 = a).
Пример:
√9 = 3 (9 > 0, 3 > 0, 32 = 9)
При а < 0 выражение √a не имеет смысла.
Пример:
√-25 – невозможно извлечь корень: 52 = 25 и -52 = 25 (а не -25)
При любом а, при котором выражение √a имеет смысл, верно равенство (√a)2 = |а|.
Пример:
(√25)2 = 52 = 25
√-52 = √25 = 5
Свойства арифметического квадратного корня: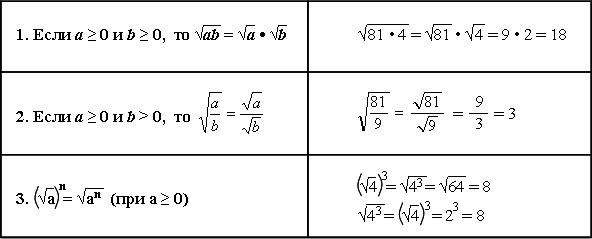
Арифметические корни n-й степени.
4√81 = 3 (так как 34 = 81)
Читается так: корень четвертой степени из 81 равен 3.
Преобразование выражений с квадратными корнями.



