Рациональные неравенства с одной переменной. Метод интервалов.

Рациональные неравенства с одной переменной – это неравенства вида f(x) > 0, f(x) < 0, f(x) ≥ 0, f(x) ≤ 0,
где f(x) – рациональное выражение.

Рациональные неравенства удобно решать методом интервалов.

Алгоритм решения рациональных неравенств методом интервалов:

Пример. Решить неравенство (х + 3) (х – 1) < 0.

Решение.

Следуем алгоритму.

1) Вводим функцию для левой части:

у = (х + 3) (х – 1).

2) Областью определения функции является все множество Х (Х ∈ R)

3) Вычисляем корни функции. То есть находим такие значения х,
при которых у = 0. Для этого каждый множитель приравниваем к нулю и вычисляем их корни:

х + 3 = 0;

х – 1 = 0.

Отсюда:

х = –3; х = 1.

4) Выделяем интервалы знакопостоянства. Для этого на оси х отмечаем наши точки (рис.1). У нас получилось три интервала:

(-∞; -3), (-3; 1), (1; +∞)

5) Чтобы определить знаки функции в каждом интервале, составим таблицу значений х (см.таблицу, рис.3):

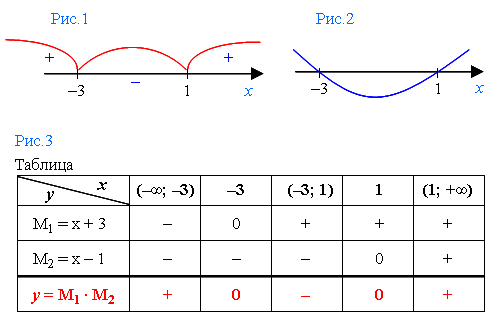
Пояснения:

Числа –3 и 1 мы выписали в отдельный столбик, потому что они тоже являются значениями х, и их тоже надо учитывать. В интервалах они не учтены, потому что, напомним правило, интервал не включает в себя конечные точки.

Первый множитель х + 3 равен нулю при х = –3. Поэтому под –3 в строке множителя М₁ пишем 0. Естественно, слева от нуля значения х отрицательные, справа от нуля – положительные. Вписываем эти знаки.

Второй множитель х – 1 равен нулю при х = 1. Поэтому под 1 в строке множителя М₂ пишем 0. Слева от 0 пишем знаки минус, справа – знак плюс.

В строке у = М₁ · М₂ подводим итоги по знакам.

Под интервалом (–∞;–3) у нас два знака минус. А произведение двух минусов дает плюс.
Следовательно, под этим интервалом в строке у = М₁ · М₂ пишем +. Это значит, что в интервале (–∞;–3) функция положительна. Отмечаем это и на графике.

Под –3 у нас один из множителей равен нулю. А произведение двух чисел, из которых одно равно нулю, есть ноль. Значит, функция равна нулю. Пишем 0.

Под интервалом (–3; 1) у нас плюс и минус. Произведение минуса и плюса дает минус. Следовательно, пишем минус. Это значит, что в интервале (–3; 1) функция у = М₁ · М₂ отрицательна. Отмечаем это и на графике.

Под 1 у нас один из множителей равен нулю – значит, и вся функция опять равна нулю. Пишем 0.

И наконец, в интервале (1; +∞) у нас оба множителя дают положительные значения – значит, функция положительная. Пишем + в таблице и на графике.

Теперь мы легко можем нарисовать и примерный вид графика. Это кривая, пересекающаяся с осью х в точках -3 и 1 (рис.2).

6) Но главное, мы, наконец, можем уже определить значения х, при которых функция меньше нуля. Мы видим, что в интервале (–3; 1) произведением двух множителей являются отрицательные числа – то есть числа, которые меньше нуля. Значит, числа, входяшие в этот интервал, и являются решением нашего неравенства.

Ответ: (х + 3) (х – 1) < 0 при х ∈ (–3; 1).

Есть еще один способ выяснения знака функции - метод пробной точки.

Принцип прост: достаточно в каждом интервале вычислить значение лишь одной любой точки – знак этого числа и окажется знаком всего интервала.

Порядок таков. В каждом интервале произвольно выбираем любую точку и вычисляем ее значение. Например, в нашем примере в первом интервале выбираем точку –4. Подставляем это число вместо х и выясняем знак:

у(–4) = (–4 + 3)( –4 – 1) > 0.

Важный вывод: это значит, что не только в точке –4, но и во всех точках интервала (–∞;–3) функция положительна. Можете это проверить, подставив несколько других значений х из интервала (–∞;–3): все значения функции будут положительные.

Точно так же вычисляем знаки функции в двух других интервалах.

Ответ будет тот же: х ∈ (–3; 1).

ПРИМЕЧАНИЕ:

Если бы было задано неравенство (х + 3) (х – 1) > 0, то ответом было бы объединение двух множеств:

х ∈ (–∞;–3) U (1; +∞).

Если бы было задано неравенство (х + 3) (х – 1) ≤ 0, то ответ получился бы таким:

х ∈ (–∞;–3] U х = –3; 1.