Линейная функция. Прямая пропорциональность. Обратная пропорциональность.
Линейная функция
Линейная функция – это функция, которую можно задать формулой y = kx + b,
где x – независимая переменная, k и b – некоторые числа.
Графиком линейной функции является прямая.
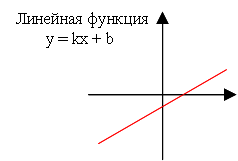 Число k называют угловым коэффициентом прямой – графика функции y = kx + b.
Число k называют угловым коэффициентом прямой – графика функции y = kx + b.
Если k > 0, то угол наклона прямой y = kx + b к оси х острый; если k < 0, то этот угол тупой.
Если угловые коэффициенты прямых, являющихся графиками двух линейных функций, различны, то эти прямые пересекаются. А если угловые коэффициенты одинаковы, то прямые параллельны.
График функции y = kx + b, где k ≠ 0, есть прямая, параллельная прямой y = kx.
Прямая пропорциональность.
Прямой пропорциональностью называется функция, которую можно задать формулой y = kx, где х – независимая переменная, k – не равное нулю число. Число k называют коэффициентом прямой пропорциональности.
График прямой пропорциональности представляет собой прямую, проходящую через начало координат (см.рисунок).
Прямая пропорциональность является частным случаем линейной функции.
Свойства функции y = kx:
1. Область определения функции - множество всех действительных чисел. 2. Это нечетная функция. 3. Переменные изменяются прямо пропорционально на всей числовой прямой: при возрастании аргумента функция пропорционально возрастает, при убывании аргумента функция пропорционально убывает. |

Обратная пропорциональность
Обратной пропорциональностью называется функция, которую можно задать формулой:
k
y = —
x
где x – независимая переменная, а k – не равное нулю число.
Графиком обратной пропорциональности является кривая, которую называют гиперболой (см.рисунок).
Для кривой, которая является графиком этой функции, оси x и y выступают в роли асимптот. Асимптота – это прямая, к которой приближаются точки кривой по мере их удаления в бесконечность.
k
Свойства функции y = —:
x
1. Область определения функции - множество всех действительных чисел, кроме нуля. 2. Это нечетная функция. 3. При возрастании аргумента функция пропорционально убывает, при убывании аргумента функция пропорционально возрастает. |


