Квадратичная функция. Функция y = ax2, ее график и свойства
Квадратичная функция – это функция, которую можно задать формулой вида
y = ax2 + bx + c,
где x – независимая переменная, a, b и c – некоторые числа, причем а ≠ 0.
Областью определения квадратичной функции является множество всех чисел. (Напомним: областью определения функции называется совокупность значений независимой переменной, см.раздел "Функции и их графики")
Функция y = ax2.
Функция y = ax2 – это частный случай квадратичной функции.
Графиком функции y = ax2 является парабола.
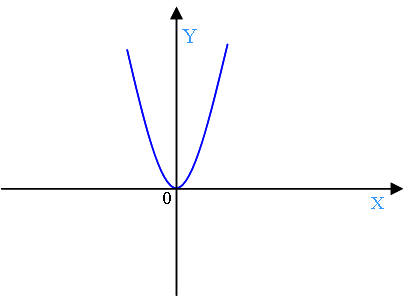
Свойства функции y = ax2 при a > 0:
1. Если x = 0, то y = 0. График функции проходит через начало координат.
2. Если x ≠ 0, то y > 0. График функции расположен в верхней полуплоскости.
3. Противоположным значениям аргумента соответствуют равные значения функции. Пояснение: допустим, x = –2, y = 8. При x = 2 значение y не меняется и составляет 8.
4. В промежутке (–∞; 0] функция убывает, а в промежутке [0; +∞) - возрастает.
5. Наименьшее значение функции равно нулю. Это значение она принимает при x = 0 (см.пункт 1). Наибольшего значения функция не имеет. Т.е. областью значений функции является промежуток [0; +∞). |
Свойства функции y = ax2 при a < 0:
1. Если x = 0, то y = 0. График функции проходит через начало координат.
2. Если x ≠ 0, то y < 0. График функции расположен в нижней полуплоскости.
3. Противоположным значениям аргумента соответствуют равные значения функции. График функции представляет собой симметричную фигуру относительно оси y. Пояснение: допустим, x = –4, y = –8. При x = 4 значение y не меняется и составляет –8.
4. В промежутке (–∞; 0] функция возрастает, а в промежутке [0; +∞) - убывает.
5. Наибольшее значение функции равно нулю. Это значение она принимает при x = 0 (см.пункт 1). Наименьшего значения функция не имеет. Т.е. областью значений функции является промежуток (–∞; 0]. |


