Функции y = ax2 + n, y = a(x – m)2, y = a(x – m)2 + n
График функции y = ax2 + n.
Графиком функции y = ax2 + n является парабола, которую можно получить из графика функции y = ax2 с помощью параллельного переноса вдоль оси y на n единиц вверх, если n > 0, или на –n единиц вниз, если n < 0. |
Пояснение.
Например, надо построить график функции y = 2x2 + 4.
Это значит, что парабола, которая является графиком функции y = 2x2, перемещается на четыре единицы вверх по оси y. Разумеется, при этом все значения y закономерно увеличиваются на 4.
Вот таблица значений функции y = 2x2:
x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
y | 32 | 18 | 8 | 2 | 0 | 2 | 8 | 18 | 32 |
А вот таблица значений y = 2x2 + 4:
x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
y | 36 | 22 | 12 | 6 | 4 | 6 | 12 | 22 | 36 |
Мы видим по таблице, что вершина параболы второй функции на 4 единицы выше вершины параболы первой (ее координаты 0;4). А значения y второй функции на 4 больше значений y первой функции.
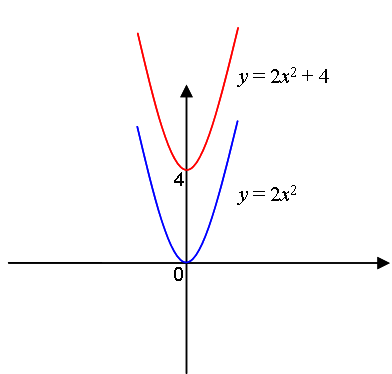
График функции y = a(x – m)2.
Графиком функции y = a(x – m)2 является парабола, которую можно получить из графика функции y = ax2 с помощью параллельного переноса вдоль оси x на m единиц вправо, если m>0, или на –m, если m<0. |
Пояснение.
Например, надо построить график функции y = 2(x – 6)2.
Это значит, что парабола, которая является графиком функции y = 2x2, перемещается на шесть единиц вправо вдоль оси x (на графике – красная парабола).
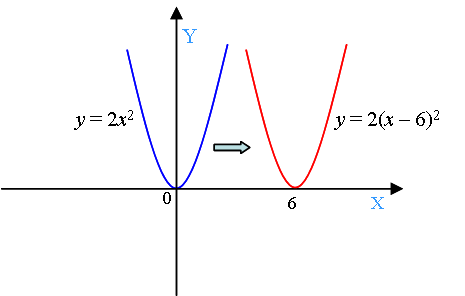
График функции y = a(x – m)2 + n.
Две функции приводят нас к третьей функции: y = a(x – m)2 + n.
Графиком функции y = a(x – m)2 + n является парабола, которую можно получить из графика функции y = ax2 с помощью двух параллельных переносов: сдвига вдоль оси x на m единиц вправо или влево и сдвига вдоль оси y на n единиц вверх или вниз. |
Пояснение:
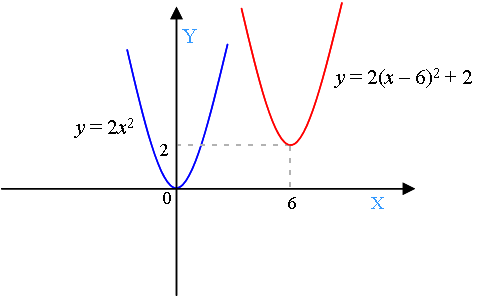
Например, надо построить график функции y = 2(x – 6)2 + 2.
Это значит, что парабола, которая является графиком функции y = 2x2, перемещается на 6 единиц вправо (значение m) и на 2 единицы вверх (значение n). Красная парабола на графике – результат этих перемещений.