Построение графика квадратичной функции
Возьмем формулу квадратичной функции y = ax2 + bx + c. Проведя вычисления, можно прийти к другому виду этой формулы (можете вычислить сами):
b b2 – 4ac
y = a(x + — )2 – ————.
2a 4a
Заменим полученные дроби буквами m и n. Тогда мы получим формулу, которая уже известна нам из предыдущего раздела:
y = a(x – m)2 + n, где
b
m = – ——,
2a
b2 – 4ac
n = – ————
4a
Вывод:
Графиком функции y = ax2 + bx + c является парабола, которую можно получить из графика функции y = ax2 с помощью двух параллельных переносов - сдвига вдоль оси x вправо или влево, а вдоль оси y – вверх или вниз.
b b2 – 4ac
Вершиной этой параболы является (m; n), где m = – ——, n = – ————.
2a 4a
Три особенности этой параболы:
1) x = m (пояснение: ось симметрии параболы параллельна оси y)
2) y = n (пояснение: y = ax2 + bx + c = a(x – m)2 + n = n)
3) при a > 0 ветви параболы направлены вверх, при a<0 – вниз.
Чтобы построить график квадратичной функции, надо в первую очередь найти координаты вершины параболы.
Пример.
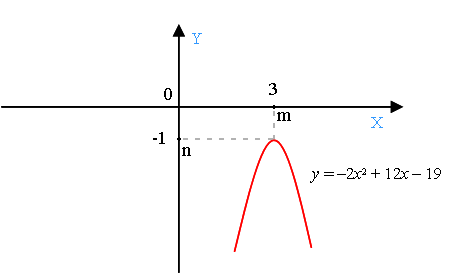
Надо построить график функции y = –2x2 + 12x – 19.
Начинаем решать. Для этого отметим, что a = –2, b = 12, c = –19.
Мы видим, что a < 0. Значит, графиком данной функции является парабола, ветви которой направлены вниз.
Найдем координаты ее вершины – то есть значения m и n:
b 12
m = – —— = – ———— = 3
2a 2 · (–2)
Значение n можно вычислить двумя способами. Один из них – формула, приведенная выше. Но поскольку x = m, а y = n (см.выше), то можно найти n более простым способом – непосредственно с помощью нашего выражения –2x2 + 12x – 19, вставляя вместо x значение m, равное 3:
n = –2 · 32 + 12 · 3 – 19 = –1
Итак, вершина параболы имеет координаты (3; –1).
Далее с помощью приведенных формул просто находим координаты еще нескольких точек, отмечаем их на оси координат, соединяем точки – и получаем нашу параболу.