Степенная функция
Степенная функция – это функция вида y = xn
(где x – независимая переменная, n – натуральное число).
Свойства степенной функции различаются в зависимости от того, четным или нечетным является значение n.
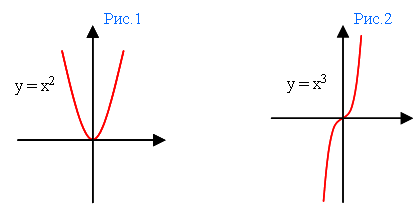
Свойства степенной функции y = xn при четном значении n.
Графиком функции является парабола, расположенная в положительной полуплоскости координат (рис.1).
1. Если x = 0, то y = 0.
График функции проходит через начало координат. 2. Если x ≠ 0, то y > 0.
График функции расположен в верхней полуплоскости. 3. Противоположным значениям аргумента соответствуют равные значения функции.
Пояснение: допустим, x = –2, y = 4. При x = 2 значение y не меняется и составляет 4. 4. В промежутке (–∞; 0] функция убывает, а в промежутке [0; +∞) - возрастает. 5. Областью значений функции являются неотрицательные числа от 0 до +∞. |
Свойства степенной функции y = xn при нечетном значении n.
Графиком функции является винтообразная кривая (рис.2).
1. Если x = 0, то y = 0.
График функции проходит через начало координат. 2. Если x > 0, то y > 0.
Если x < 0, то y < 0.
График функции проходит через первую и третью координатные четверти. 3. Противоположным значениям аргумента соответствуют противоположные значения функции.
Пояснение: возьмем функцию y = x3. Если x = 2, то y = 8. Если x = –2, то y = –8. 4. На всей области определения функция возрастает. 5. Областью значения функции является множество всех действительных чисел. |
