Арксинус

Арксинус  в переводе с латинского означает дуга и синус. Это обратная функция.

Говоря иначе:

Пример-пояснение:
Найдем arcsin 1/2.

Решение.
Выражение arcsin 1/2 показывает, что синус угла t равен 1/2 (sin t = 1/2).

Далее просто находим точку этого синуса на числовой окружности, что и является ответом:

точка 1/2, находящася на оси у,  соответствует точке π/6 на числовой окружности.
Значит, arcsin 1/2 = π/6.

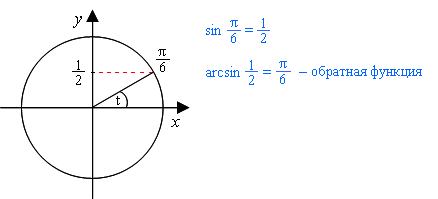
Обратите внимание:

если sin π/6 = 1/2, то arcsin 1/2 = π/6.

То есть в первом случае по точке на числовой окружности находим значение синуса, а во втором – наоборот, по значению синуса находим точку на числовой окружности. Движение в обратную сторону. Это и есть арксинус.

Формулы.

(1)

 
(2)

                                                       √2
Пример 1: Вычислить arcsin (– ——).
                                                        2

Решение.

Решая пример, следуем буквально по таблице над нашим примером.

Итак:

           √2
а = – ——.
            2

                           √2
Тогда sin t = – ——, при этом t входит в отрезок [–π/2; π/2]
                            2

                        π
Значит t = – —— (входит в отрезок [–π/2; π/2])
                        4

                            √2            π
Ответ: arcsin (– ——) = – —
                             2             4

Акцентируем ваше внимание: синусом числа –π/4 является -√2/2, а арксинусом -√2/2 является –π/4. Движение в обратном порядке. Cинусом числа является точка на оси координат, а арксинусом – точка на числовой окружности.

                                                  √3
Пример 2: Вычислить arcsin ——
                                                   2

Решение.

                       √3
Пусть arcsin —— = t.
                        2

                        √3
Тогда sin t = ——.
                         2

Точка t находится в отрезке [–π/2; π/2]. Вычисляем значение t.

              √3
Число —— соответствует значению sin π/3, при этом π/3 находится в отрезке [–π/2; π/2].
              2

Значит:

t = π/3.

Итог:

            √3
arcsin —— = π/3.
             2

Пример решен.