Приращение аргумента и функции
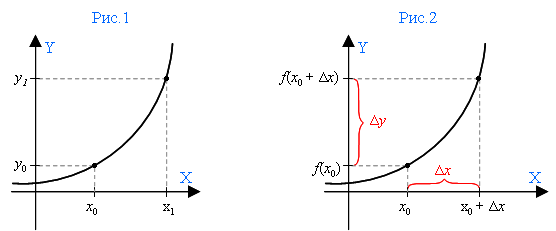
На оси Х – две точки: x0 и x1 (рис.1). Если от x1 отнимем x0, то узнаем длину шага между ними – а говоря иначе, узнаем, на сколько приросла точка x0 в точке x1. Эта разность между двумя заданными точками оси X и называется приращением аргумента.
Точки x0 и x1 образуют на оси Y соответственно точки у0 и у1. Если от у1 отнять у0, то мы получим приращение функции.
Итак, в функции y = f(x) относительно определенных точек x0 и x1:
разность x1 – x0 называется приращением аргумента, а разность у1 – у0 называется приращением функции.
Но у0 и у1 – зависимые переменные (зависимые от значений х). То есть их правильно записывать так: f(x0) и f(x1). Следовательно, приращение функции – это разность f(x1) – f(x0).
Приращение обозначается греческой буквой Δ (дельта):
Δx = x1 – x0;
Δy (или Δ f) = f(x1) – f(x0).
Можно сказать и иначе: если к x0 прибавить величину приращения Δx, то мы получим точку x1.
То есть x1 = x0 + Δx (рис.2).
Тогда точку f(x1), отмеченную на первом рисунке как у1, тоже можно обозначить иначе:
f(x0 + Δx).
Осталось вывести формулу приращения функции.
Формула приращения функции:
Δy = f(x0 + Δx) – f(x0) или Δf = f(x0 + Δx) – f(x0) |
Пример: Дана функция y = x2. На оси абсцисс – две точки:
х0 = 3,
(х0 + Δx) = 4.
Надо найти приращение функции при переходе от точки х0 к точке (х0 + Δx).
Решение.
Итак, мы хотим найти Δy.
Сначала определимся с функцией:
так как у = f(x), то f(x) = x2.
Теперь вычисляем приращение аргумента:
Δx = (х0 + Δx) – х0 = 4 – 3 = 1
Находим значения функции при х0 = 3 и (х0 + Δx) = 4:
f(x0) = f(3) = 32 = 9
f(x0 + Δx) = f(4) = 42 = 16
Осталось найти приращение функции:
Δy = f(x0 + Δx) – f(x0) = f(4) – f(3) = 16 – 9 = 7.
Ответ: Δy = 7.


