Производная функции. Дифференцирование. Алгоритм вычисления производной

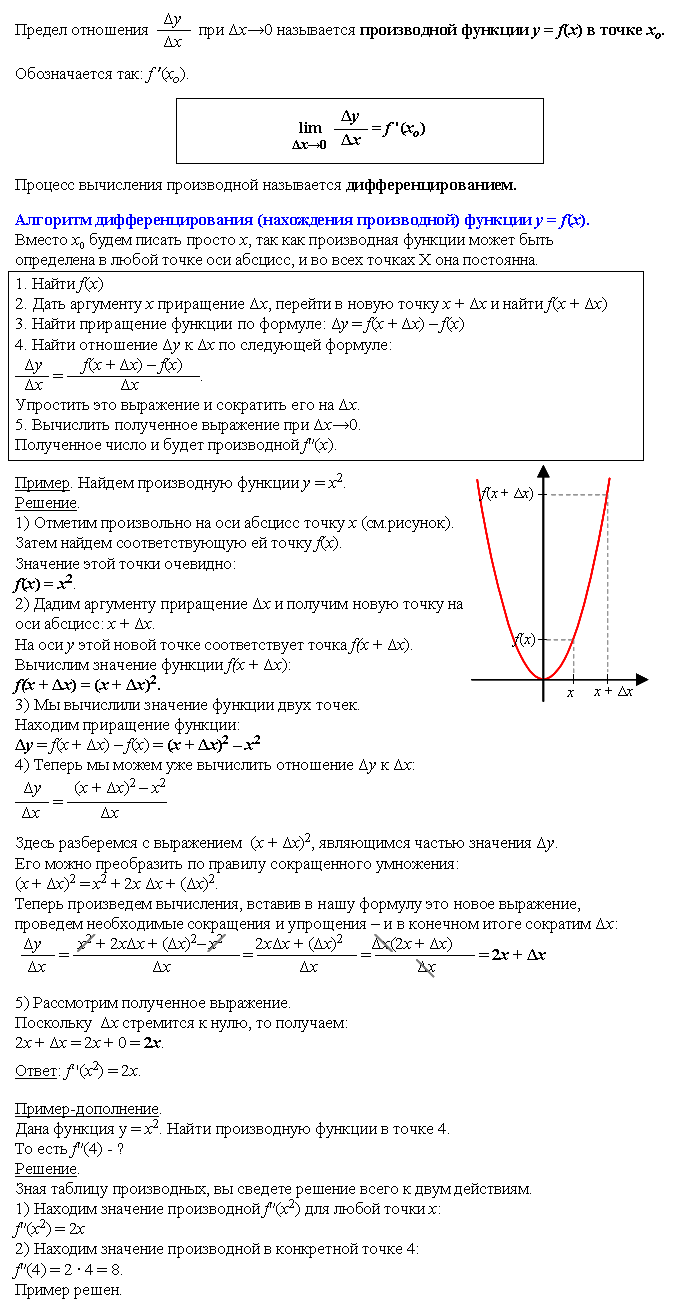
Чтобы понять производную, зададим некоторую функцию y = f(x). Пусть графиком этой функции является некоторая кривая (см.рисунок).

1) На оси X отметим произвольно точку х_о. На оси Y ей соответствует точка f(x_о). Точку пересечения двух координат  назовем А.

2) Дадим точке х_о приращение Δx и получим новую точку на оси абсцисс: х_о + Δx. Повторим те же действия: получим на кривой вторую точку В, а на оси ординат отметим соответствующую точку: f(x_о + Δx). Разница между двумя точками оси у – это приращение функции Δу. То есть:

Δy = f(x_о + Δx) – f(x_о).

3) Проведем секущую через точки А и В.

   4) Устремим приращение Δх к нулю – то есть к точке х_о. Тогда наша секущая начнет поворачиваться, при этом точка В будет неуклонно приближаться по кривой к точке А. Приращение функции Δy тоже устремится к нулю, а секущая достигнет того предельного положения, когда с кривой графика функции у нее окажется одна-единственная общая точка А. Секущая превратится в касательную к графику функции в точке х_о. То есть в точке х_о будет достигнут некий уникальный предел в отношениях между Δy и Δх. При этом Δy и Δх не равны нулю, но являются бесконечно малыми величинами. Если ось Х принять за шкалу времени t, то Δх в точке х_о будет мгновением, близким к нулю. Если же ось Y принять за шкалу расстояния S, то в точке f(x_о) мы получим расстояние, которое прошло тело в момент времени х_о. А разделив Δy на Δх в точке x_о, мы получим ничто иное как мгновенную среднюю скорость в момент времени х_о (V = S : t). Так мы попутно определили физический смысл этого явления. В математике оно имеет другое имя: это и есть производная. Ее называют скоростью изменения функции в данной точке.