Треугольники

 

Основные понятия.

Треугольник – это фигура, состоящая из трех отрезков и трех точек, не лежащих на одной прямой.

Отрезки называются сторонами, а точки – вершинами.

Любая сторона любого треугольника меньше суммы двух других сторон, но больше их разности. a – b < c < a + b

 
Высота треугольника – это перпендикуляр, проведенный из вершины  к противолежащей стороне (рис.1).

Биссектриса треугольника – это отрезок, который делит угол вершины пополам и соединяет вершину с точкой на противолежащей стороне (рис.2).

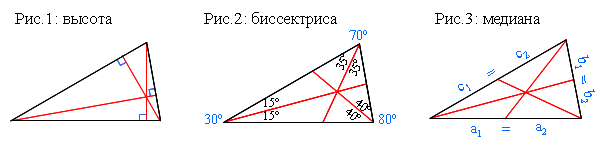
Медиана треугольника.

Медиана треугольника – это отрезок, соединяющий вершину с серединой противолежащей стороны (рис.3). Длину медианы можно вычислить по формуле:                                                                       2b2 + 2c2 – a2                                                             ma2 = ——————                                                                                 4 где ma – медиана, проведенная к стороне а. В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы:                                                                                       c                                                                             mc = —                                                                                       2 где mc – медиана, проведенная к гипотенузе c (рис.6) Медианы треугольника пересекаются в одной точке (в центре масс треугольника) и делятся этой точкой в соотношении 2:1, отсчитывая от вершины. То есть отрезок от вершины к центру в два раза больше отрезка от центра к стороне треугольника. Три медианы треугольника делят его на шесть равновеликих треугольников.

Средняя линия треугольника – это отрезок, соединяющий середины двух его сторон. Она параллельна третьей стороне и равна ее половине (рис.4).

Сумма углов треугольника равна 180^º.

Внешний угол треугольника равен сумме двух несмежных внутренних углов (рис.5).

Внешний угол треугольника больше любого несмежного угла.

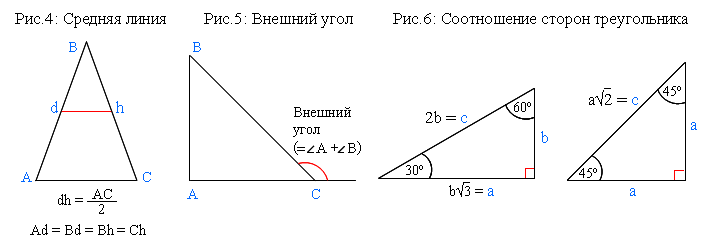     Прямоугольный треугольник.

Прямоугольный треугольник – это треугольник, у которого есть прямой угол (рис.7).

Сторона прямоугольного треугольника, противолежащая прямому углу, называется гипотенузой. Две другие стороны называются катетами.

  
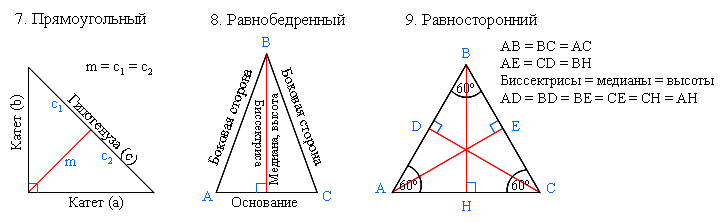
Равнобедренный треугольник.

Равнобедренный треугольник – это треугольник, у которого две стороны равны (рис.8).

Эти равные стороны называются боковыми сторонами, а третья – основанием треугольника.

В равнобедренном треугольнике углы при основании равны. (В нашем треугольнике угол А равен углу C).

В равнобедренном треугольнике медиана, проведенная к основанию, является одновременно и биссектрисой, и высотой треугольника.

 

Равносторонний треугольник.

Равносторонний треугольник – это треугольник, у которого все стороны равны (рис.9).

Свойства равностороннего треугольника:

1) все углы равны 60º; 2) медианы, биссектрисы и высоты совпадают; 3) медианы, биссектрисы и высоты соединяют вершины с серединами противолежащих сторон.

Замечательные свойства треугольников

У треугольников есть оригинальные свойства, которые помогут вам успешно решать задачи, связанные с этими фигурами. Некоторые из этих свойств изложены выше. Но повторяем их еще раз, добавив к ним несколько других замечательных особенностей:

1) В прямоугольном треугольнике с углами 90º, 30º и 60º катет b, лежащий напротив угла в 30º, равен половине гипотенузы. А катет  a больше катета b в √3 раз (рис.6). К примеру, если катет b равен 5, то гипотенуза c обязательно равна 10, а катет а равен 5√3.  2) В прямоугольном равнобедренном треугольнике с углами 90º, 45º и 45º гипотенуза в √2 раз больше катета (рис.6). К примеру, если катеты равны 5, то гипотенуза равна 5√2. 3) Средняя линия треугольника равна половине параллельной стороны (рис.4). К примеру, если сторона треугольника равна 10, то параллельная ей средняя линия равна 5.  4) В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы (рис.7): mc =  с/2. 5) Медианы треугольника, пересекаясь в одной точке, делятся этой точкой в соотношении 2:1. То есть отрезок от вершины к точке пересечения медиан в два раза больше отрезка от точки пересечения медиан к стороне треугольника (рис.3) 6) В прямоугольном треугольнике середина гипотенузы является центром описанной окружности.

Признаки равенства треугольников.

Первый признак равенства: если две стороны и угол между ними одного треугольника равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Второй признак равенства: если сторона и прилежащие к ней углы одного треугольника равны стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.

Третий признак равенства: если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.

 

Неравенство треугольника.

В любом треугольнике каждая сторона меньше суммы двух других сторон.

 

Теорема Пифагора.

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:

c² = a² + b².

Площадь треугольника.

1) Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне:

         ah
S = ——
          2

2) Площадь треугольника равна половине произведения двух любых его сторон на синус угла между ними:

       1
S = — AB · AC · sin A
        2

 

Синус, косинус, тангенс, котангенс острого угла треугольника.

Синус острого угла α прямоугольного треугольника – это отношение противолежащего катета к гипотенузе.
Обозначается так: sin α.

Косинус острого угла α прямоугольного треугольника – это отношение прилежащего катета к гипотенузе.
Обозначается так: cos α.

Тангенс острого угла α – это отношение противолежащего катета к прилежащему катету.
Обозначается так: tg α.

Котангенс острого угла α – это отношение прилежащего катета к противолежащему.
Обозначается так: ctg α.

 

Правила:

Катет, противолежащий углу α, равен произведению гипотенузы на sin α.

Катет, прилежащий к углу α, равен произведению гипотенузы на cos α.

Катет, противоположный углу α, равен произведению второго катета на tg α.

 

Основные тригонометрические тождества:

                  sin α
1)    tg α = ——
                  cos α

 

2)    sin² α + cos² α = 1

 

                           1
3)    1 + tg² α = ——
                         cos² α

 

                1             1
4)    1 + ——  =  ——
              tg² α       sin² α

 

Для любого острого угла α:

sin (90° – α) = cos α

cos (90° – α) = sin α

 

При возрастании острого угла sin α и tg α возрастают, а cos α убывает.