Дробно-линейная функция и ее график
ax + b
Дробно-линейная функция – это функция вида y = ——— ,
cx + d
где x – переменная, a, b, c, d – некоторые числа, причем c ≠ 0, ad – bc ≠ 0.
Свойства дробно-линейной функции:
1. При возрастании положительных значений аргумента значения функции убывают и стремятся к нулю, но остаются положительными. 2. При возрастании положительных значений функции значения аргумента убывают и стремятся к нулю, но остаются положительными. |
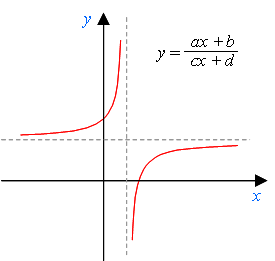
Графиком дробно-линейной функции является гипербола, которую можно получить из гиперболы y = k/x с помощью параллельных переносов вдоль координатных осей. Для этого формулу дробно-линейной функции надо представить в следующем виде:
k
y = n + ———
x – m
где n – количество единиц, на которое гипербола смещается вправо или влево, m – количество единиц, на которое гипербола смещается вверх или вниз. При этом асимптоты гиперболы сдвигаются в прямые x = m, y = n.
Асимптота – это прямая, к которой приближаются точки кривой по мере их удаления в бесконечность (см.рисунок ниже).
Что касается параллельных переносов – см.предыдущие разделы.
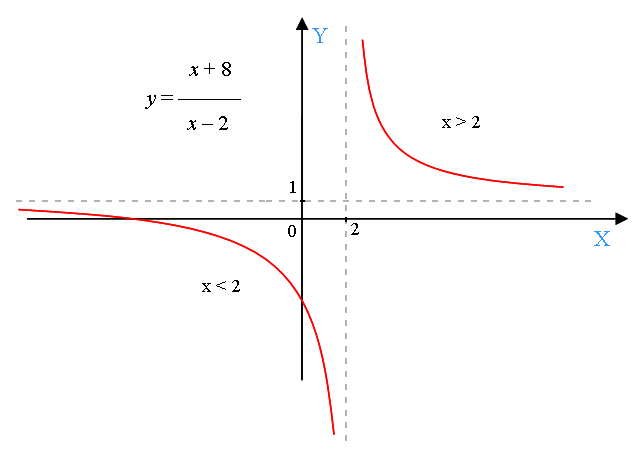
Пример 1. Найдем асимптоты гиперболы и построим график функции:
x + 8
y = ———
x – 2
Решение:
k
Представим дробь в виде n + ———
x – m
Для этого x + 8 запишем в следующем виде: x – 2 + 10 (т.е. 8 представили в виде –2 + 10).
Получим:
x + 8 x – 2 + 10 1(x – 2) + 10 10
——— = ————— = —————— = 1 + ———
x – 2 x – 2 x – 2 x – 2
Почему выражение приняло такой вид? Ответ простой: произведите сложение (приведя оба слагаемых к общему знаменателю), и вы вернетесь к предыдущему выражению. То есть это результат преобразования заданного выражения.
Итак, мы получили все необходимые значения:
k = 10, m = 2, n = 1.
Таким образом, мы нашли асимптоты нашей гиперболы (исходя из того, что x = m, y = n):
x = 2, y = 1.
То есть одна асимптота гиперболы проходит параллельно оси y на расстоянии 2 единиц справа от нее, а вторая асимптота проходит параллельно оси x на расстоянии 1 единицы выше ее.
Построим график данной функции. Для этого сделаем следующее:
1) проведем в координатной плоскости пунктиром асимптоты – прямую x = 2 и прямую y = 1.
2) так как гипербола состоит из двух ветвей, то для построения этих ветвей составим две таблицы: одну для x<2, другую для x>2.
Сначала подберем значения x для первого варианта (x<2). Если x = –3, то:
10
y = 1 + ——— = 1 – 2 = –1
–3 – 2
Выбираем произвольно другие значения x (например, -2, -1, 0 и 1). Вычисляем соответствующие значения y. Результаты всех полученных вычислений вписываем в таблицу:
x | -3 | -2 | -1 | 0 | 1 |
y | -1 | -1,5 | -2,3 | -4 | -9 |
Теперь составим таблицу для варианта x>2:
x | 3 | 4 | 5 | 6 | 7 |
y | 11 | 6 | 4,3 | 3,5 | 3 |
3) Далее просто составляете график функции с полученными координатами.