Функция y = ln x
Графиком функции y = ln x является экспонента, у которой в точке х = 1 угол между касательной и осью абсцисс равен 45º.
Не следует путать с функцией у = ех, у которой: а) касательная под углом 45º пересекает ось абсцисс в точке х = 0; б) экспонента выпукла вниз.
В отличие от функции у = ех, экспонента функции y = ln x выпукла вверх.
График функции y = ln x симметричен графику функции у = ех относительно прямой у = х.
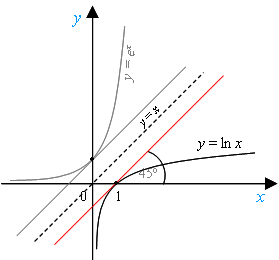
Свойства функции y = ln x:
1) Областью определения являются все положительные числа: D(f) = (0; +∞). 2) Область значений функции – все числа от –∞ до +∞: E(f) = (–∞; +∞) 3) Функция ни четная, ни нечетная. 4) Возрастает на промежутке (0; +∞). 5) Не ограничена ни снизу, ни сверху. 6) Не имеет наибольшего и наименьшего значений. 7) Непрерывна. 8) Выпукла вверх. 9) Дифференцируема. |
Производная функции y = ln x:
1 |


