Тригонометрические функции числового и углового аргументов

Тригонометрические функции числового аргумента.

Тригонометрические функции числового аргумента t  – это функции вида y = cos t,
y = sin t, y = tg t, y = ctg t.

С помощью этих формул через известное значение одной тригонометрической функции можно найти неизвестные значения других тригонометрических функций.

Пояснения.

1) Возьмем формулу cos² t + sin² t = 1 и выведем с ее помощью новую формулу.

Для этого разделим обе части формулы на cos² t (при t ≠ 0, то есть t ≠ π/2 + πk). Итак:

  cos² t        sin² t             1
——— + ———  =  ———
 cos² t        cos² t          cos² t

Первое слагаемое равно 1. Мы знаем, что отношение синуса к конисусу – это тангенс, значит, второе слагаемое равно tg² t. В результате мы получаем новую (и уже известную вам) формулу:

2) Теперь разделим cos² t + sin² t = 1 на sin² t (при t ≠ πk):

  cos² t        sin² t             1
——— + ———  =  ———,   где t ≠ πk + πk, k – целое число
  sin² t         sin² t          sin² t

Отношение косинуса к синусу – это котангенс. Значит:

Зная элементарные основы математики и выучив основные формулы тригонометрии, вы легко сможете самостоятельно выводить большинство остальных тригонометрических тождеств. И это даже лучше, чем просто зазубривать их: выученное наизусть быстро забывается, а понятое запоминается надолго, если не навсегда. К примеру, необязательно зазубривать, чему равна сумма единицы и квадрата тангенса. Забыли – можно легко вспомнить, если вы знаете самую простую вещь: тангенс – это отношение синуса к косинусу. Примените вдобавок простое правило сложения дробей с разными знаменателями – и получите результат:

                           sin² t         1         sin² t          cos² t + sin² t             1
1 + tg² t  =  1 + ———  =  —  +  ———  =  ——————  =  ———
                          cos² t         1          cos² t               cos² t                cos² t

Точно так же легко можно найти сумму единицы и квадрата котангенса, как и многие другие тождества.

Тригонометрические функции углового аргумента.

В функциях  у = cos t, у = sin t, у = tg t, у = ctg t переменная t может быть не только числовым аргументом. Ее можно считать и мерой угла – то есть угловым аргументом.

С помощью числовой окружности и системы координат можно легко найти синус, косинус, тангенс, котангенс любого угла. Для этого должны быть соблюдены два важных условия:
1) вершиной угла должен быть центр окружности, который одновременно является центром оси координат;

2) одной из сторон угла должен быть положительный луч оси x.

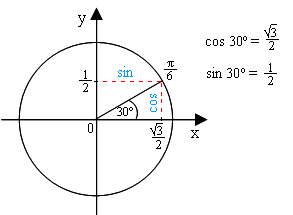
В этом случае ордината точки, в которой пересекаются окружность и вторая сторона угла, является синусом этого угла, а абсцисса этой точки – косинусом данного угла.

Пояснение. Нарисуем угол, одна сторона которого – положительный луч оси x, а вторая сторона выходит из начала оси координат (и из центра окружности) под углом 30º (см.рисунок). Тогда точка пересечения второй стороны с окружностью соответствует π/6. Нам известны ордината и абсцисса этой точки. Они же являются косинусом и синусом нашего угла:

   √3       1
 ——; ——
    2        2

  А зная синус и косинус угла, вы уже легко сможете найти его тангенс и котангенс.

Таким образом, числовая окружность, расположенная в системе координат, является удобным способом найти синус, косинус, тангенс или котангенс угла.

Но есть более простой способ. Можно и не рисовать окружность и систему координат. Можно воспользоваться простыми и удобными формулами:

Пример: найти синус и косинус угла, равного 60º.

Решение:

                        π · 60                π         √3
sin 60º  =  sin ———  =  sin —— = ——
                         180                  3          2

                           π        1
cos 60º  =  cos —— = —
                           3        2

Пояснение: мы выяснили, что синус и косинус угла 60º соответствуют значениям точки окружности π/3. Далее просто находим в таблице значения этой точки – и таким образом решаем наш пример. Таблица синусов и косинусов основных точек числовой окружности – в предыдущем разделе и на странице «Таблицы».