Экстремум функции
Определения:
Экстремумом называют максимальное или минимальное значение функции на заданном множестве.
Точка экстремума – это точка, в которой достигается максимальное или минимальное значение функции.
Точка максимума – это точка, в которой достигается максимальное значение функции.
Точка минимума – это точка, в которой достигается минимальное значение функции.
Пояснение.
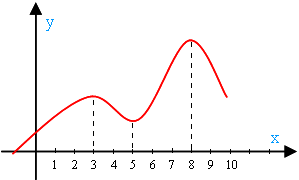
На рисунке в окрестности точки х = 3 функция достигает максимального значения (то есть в окрестности именно этой точки нет точки выше). В окрестности х = 8 она опять же имеет максимальное значение (снова уточним: именно в этой окрестности нет точки выше). В этих точках возрастание сменяется убыванием. Они являются точками максимума:
xmax = 3, xmax = 8.
В окрестности точки х = 5 достигается минимальное значение функции (то есть в окрестности х=5 точки ниже нет). В этой точке убывание сменяется возрастанием. Она является точкой минимума:
xmin = 5.
Точки максимума и минимума являются точками экстремума функции, а значения функции в этих точках – ее экстремумами.
Точка xо является точкой максимума, если у нее существует окрестность, во всех точках которой f(x) меньше или равно f(xо): f(x) ≤ f(xо) Упрощенная формулировка: если в точке xо производная меняет знак с плюса на минус, то xо является точкой максимума.
Точка хо является точкой минимума, если у нее существует окрестность, во всех точках которой f(x) больше или равно f(xо): f(x) ≥ f(xо) Упрощенная формулировка: если в точке xо производная меняет знак с минуса на плюс, то xо является точкой минимума. |
Критические и стационарные точки функции:
Внутренние точки области определения функции, в которых функция непрерывна, но производная не существует, называют критическими точками. Внутренние точки области определения функции, при которых производная функции равна нулю, называются стационарными точками. |
Необходимое условие экстремума:
Если xо – точка экстремума функции f (x), то в этой точке либо производная обращается в нуль (и это стационарная точка), либо производная не существует (критическая точка). |
Достаточное условие экстремума:
Пусть xо – критическая точка. Если производная f ′(x) при переходе слева направо через точку xо меняет знак плюс на минус, то xо – точка максимума: xо – точка максимума, y = f(xо) – максимум.
Если производная f ′(x) при переходе слева направо через точку xо меняет знак минус на плюс, то xо – точка минимума: xо – точка минимума, y = f(xо) – минимум.
Если при переходе через критическую точку производная не меняет знак, то в точке xо экстремума нет. |
На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b].
Алгоритм исследования непрерывной функции y = f(x) на монотонность и экстремумы:
1) Найти производную f ′(x). 2) Найти стационарные (f ′(x) = 0) и критические (f ′(x) не существует) точки функции y = f(x). 3) Отметить стационарные и критические точки на числовой прямой и определить знаки производной на получившихся промежутках. 4) Сделать выводы о монотонности функции и ее точках экстремума. |


