Углы
Основные понятия.
Угол – это фигура, образованная двумя лучами, выходящими из одной точки.
Вершина угла – это точка, из которой выходят два луча, образующих этот угол.
Биссектриса – это луч, который выходит из вершины угла и делит угол пополам.
Развернутый угол – это угол, стороны которого лежат на одной плоскости; равен 180˚ и является прямой.
Прямой угол – это угол, равный половине развернутого угла; равен 90˚.
Острый угол – это угол, который меньше прямого.
Тупой угол – это угол, который больше прямого, но меньше развернутого.
Угол разбивает плоскость на две части. Каждая из частей называется плоским углом.
Плоские углы с общими сторонами называются дополнительными.
Если плоский угол является частью полуплоскости, то его градусной мерой называется градусная мера обычного угла с теми же сторонами.
Если плоский угол содержит полуплоскость, то его градусная мера равна 360º – α, где α – градусная мера дополнительного плоского угла.
Равные углы.
Это углы, которые совпадают при наложении.
Смежные углы.
Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.
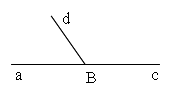На рисунке углы (ad) и (cd) смежные. У них сторона d общая, а стороны a и c – дополнительные полупрямые.
Теорема:
Сумма смежных углов равна 180º.
Из теоремы следует:
- если два угла равны, то смежные с ними углы равны.
- если угол не развернутый, то его градусная мера меньше 180º.
- угол, смежный с прямым углом, есть прямой угол.
Вертикальные углы.
Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого. Они созданы пересечением двух прямых и не являются прилегающими, имеют общую вершину и одинаковую градусную меру.
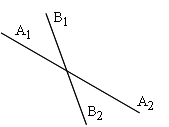На рисунке углы (A1 B1) и (A2 B2) вертикальные. Стороны A2 и B2 второго угла являются дополнительными полупрямыми сторон A1 и B1 первого угла.
Центральный угол.
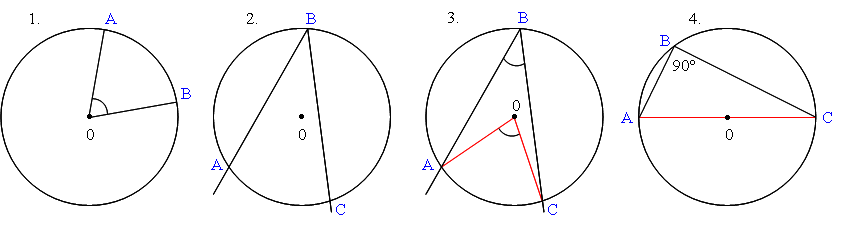
Центральным углом в окружности называется плоский угол с вершиной в ее центре (рис.1).
Часть окружности, расположенная внутри плоского угла, называется дугой окружности, соответствующей этому центральному углу (на рис.1 дуга AB является дугой окружности).
Градусной мерой дуги окружности называется градусная мера соответствующего центрального угла.
Угол, вписанный в окружность.
Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным в окружность (рис.2).
Свойства:
1) Вписанный угол равен половине соответствующего центрального угла (на рис.3 вписанный угол ABC равен половине соответствующего ему центрального угла AOC). 2) Вписанный угол, опирающийся на диаметр, равен 90° (рис.4). 3) Вписанный угол, опирающийся на хорду, равную радиусу окружности, равен 30°. |
Углы при пересечении двух прямых третьей.
При пересечении прямых a и b секущей c образуется восемь углов, которые на рисунке обозначены цифрами. Некоторые пары этих углов имеют специальные названия:
накрест лежащие углы: 3 и 5, 4 и 6;
односторонние углы: 4 и 5, 3 и 6;
соответственные углы: 1 и 5, 4 и 8, 2 и 6, 3 и 7.
