Внеклассный урок - Окружность

Окружность

Окружность – это фигура, которая состоит из всех точек плоскости, равноудаленных от данной точки.

Основные понятия:

Центр окружности – это точка, равноудаленная от точек окружности.

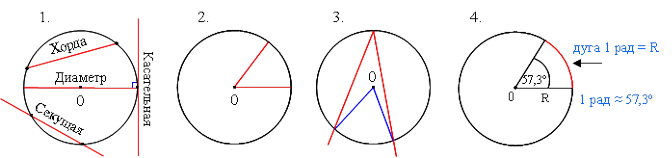
Радиус – это расстояние от точек окружности до ее центра (равен половине диаметра, рис.1).

Диаметр – это хорда, проходящая через центр окружности (рис.1).

Хорда – это отрезок, соединяющий две точки окружности (рис.1).

Касательная – это прямая, имеющая только одну общую точку с окружностью. Проходит через точку окружности перпендикулярно диаметру, проведенному в эту точку (рис.1).

Секущая – это прямая, проходящая через две различные точки окружности (рис.1).

Единичная окружность – это окружность, радиус которой равен единице.

Дуга окружности – это часть окружности, разделенная двумя несовпадающими точками окружности.

1 радиан – это угол, образуемый дугой окружности, равной длине радиуса (рис.4).
1 радиан = 180˚ : π ≈ 57,3˚

Центральный угол – это угол с вершиной в центре окружности. Равен градусной мере дуги, на которую опирается (рис.2).

Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают эту окружность. Равен половине градусной меры дуги, на которую опирается (рис.3).

Две окружности, имеющие общий центр, называются концентрическими.

Две окружности, пересекающиеся под прямым углом, называются ортогональными.

Длина окружности и площадь круга:

Обозначения:
Длина окружности – C
Длина диаметра – d
Длина радиуса – r

Значение π:
Отношение длины окружности к длине ее диаметра обозначается греческой буквой π (пи).

π = 3,1416

Или:

π = 3,14

Или:

22
π = —
7

Формула длины окружности:

C = πd, или C = 2πr

Формулы площади круга:

S = πr²

C · r
S = ——
2

π · D²
S = ———
4

Площадь кругового сектора и кругового сегмента.

Круговой сектор – это часть круга, лежащая внутри соответствующего центрального угла.
Формула площади кругового сектора:

                                                                        πR²
                                                              S = ——— α
                                                                        360

где π – постоянная величина, равная 3,1416; R – радиус круга; α – градусная мера соответствующего центрального угла.

Круговой сегмент – это общая часть круга и полуплоскости.
Формула площади кругового сегмента:

                                                                        πR²
                                                              S = ——— α ± S_Δ
                                                                        360

где α – градусная мера центрального угла, который содержит дугу этого кругового сегмента; S_Δ - площадь треугольника с вершинами в центре круга и в концах радиусов, ограничивающих соответствующий сектор.

Знак «минус» надо брать, когда α < 180˚, а знак «плюс» надо брать, когда α > 180˚.

Уравнение окружности в декартовых координатах x, y c центром в точке (a;b):

(x – a)² + (y – b)² = R²

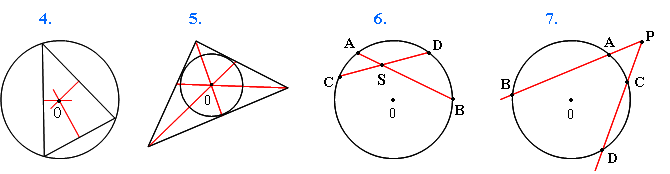
Окружность, описанная около треугольника (рис.4).

Если от середины каждой из сторон треугольника провести перпендикуляры, то точка их пересечения будет центром окружности, описанной около этого треугольника.

Окружность, вписанная в треугольник (рис.5).

Центр окружности, вписанной в треугольник, является точкой пересечения биссектрис этого треугольника.

Углы, вписанные в окружность (рис.3).

Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным в окружность.

Угол, вписанный в окружность, равен половине соответствующего центрального угла.

Основные понятия:

Угол делит плоскость на две части. Каждая из этих частей называется плоским углом.

Плоские углы с общими сторонами называются дополнительными.

Плоский угол с вершиной в центре окружности называется центральным углом (рис.2)

Пропорциональность отрезков хорд и секущих окружности.

Если хорды AB и CD окружности пересекаются в точке S, то

AS · BS = CS · DS.

(рис.6)

Если из точки P к окружности проведены две секущие, пересекающие окружность соответственно в точках A, B и C, D, то

AP · BP = CP · DP

(рис.7)

Частные случаи и формулы:

1) Из точки C, находящейся вне окружности, проведем касательную к окружности и обозначим точку их соприкосновения буквой D.

Затем из той же точки C проведем секущую и точки пересечения секущей и окружности обозначим буквами А и B (рис.8).

В этом случае:

CD² = AC · BC

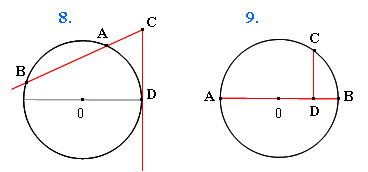
2) Проведем в окружности диаметр AB. Затем из точки C, находящейся на окружности, проведем перпендикуляр к этому диаметру и обозначим получившийся отрезок CD (рис.9).

В этом случае:

CD² = AD · BD.

Сайт создан в системе uCoz